遍历二叉树的神级方法（Morris 遍历）

题目

给定一棵二叉树的头节点 head，完成二叉树的先序、中序和后序遍历。如果二叉树的节点数为 N，则要求时间复杂度为 O(N)，额外空间复杂度为 O(1)。

解答

要想使得遍历二叉树的额外空间复杂度为 O(1)，那么就需要使用 Morris 遍历方法。

Morris 方法的思路，讲得最好的我认为是这一篇博客：https://www.cnblogs.com/anniekim/archive/2013/06/15/morristraversal.html

其中，最核心的是它讲述的步骤，Morris 遍历的原始版本其实是中序遍历，步骤如下

1. 如果当前节点的左孩子为空，则输出当前节点并将其右孩子作为当前节点。

2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点（predecessor）。找到前驱节点之后，关于前驱节点，又要分为以下两种情况来处理：

   • 2.1、如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。当前节点更新为当前节点的左孩子。

   • 2.2、如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空（恢复树的形状）。输出当前节点。当前节点更新为当前节点的右孩子。

3. 重复以上 1、2 直到当前节点为空。

下面就是 Java 代码的全部实现

原始不打印节点的版本

Node 数据结构

public class Node {
    public int value;
    public Node left;
    public Node right;

    public Node(int value) {
        this.value = value;
    }
}

// 初始版本的 morris 遍历，没有作任何打印
public void morris(Node head) {
    if (head == null) {
        return;
    }
    Node cur = head; // cur 初始时为头节点
    Node mostRight = null; // 这个其实就是当前节点 cur 的前驱节点（predecessor）
    while (cur != null) {
        mostRight = cur.left;
        if (mostRight != null) { // 如果当前 cur 有左子树
            // 找到左子树上最右边的节点，即前驱（predecessor）节点
            while (mostRight.right != null && mostRight.right != cur) {
                mostRight = mostRight.right;
            }
            // 从上面的 while 里出来后，mostRight 就是 cur 左子树上最右的节点
            if (mostRight == null) { // 如果 mostRight.right 指向 null，说明是第一次访问这个节点
                mostRight.right = cur; // 让 mostRight 的右指针指向当前 cur 节点
                cur = cur.left; // cur 向左移动
                continue; // 回到最外层的 while，继续判断 cur 的情况
            } else { // 如果 mostRight.right 是指向 cur 的
                mostRight.right = null; // 将 mostRight 的右指针指向恢复为 null
            }
        }
        // a、cur 如果没有左子树，cur 向右移动
        // b、或者 cur 左子树上最右节点的右指针是指向 cur 的，cur 向右移动
        cur = cur.right;
    }
}

前序遍历版本

// 先序遍历
public void morrisPre(Node head) {
    if (head == null) {
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while (cur != null) {
        mostRight = cur.left;
        if (mostRight != null) { // 当前节点左孩子不为 null 的情况
            while (mostRight.right != null && mostRight.right != cur) {
                mostRight = mostRight.right;
            }
            // 根据上面循环截止的两个条件，分两种情况进行处理
            if (mostRight.right == null) {
                mostRight.right = cur;
                System.out.print(cur.value + " "); // 因为是先序遍历，所以要先打印
                cur = cur.left;
                continue;
            } else {
                mostRight.right = null; // 某个节点第二次被访问时，这里不作打印操作，仅仅把 mostRight 的右指针恢复为 null
            }
        } else { // 当前节点左孩子为 null 则直接打印当前节点
            System.out.print(cur.value + " "); // 打印节点
        }
        // a、cur 如果没有左子树，cur 向右移动
        // b、或者 cur 左子树上最右节点的右指针是指向 cur 的，cur 向右移动
        cur = cur.right; // 当前节点往右走
    }
}

中序遍历版本

// 中序遍历
public void morrisIn(Node head) {
    if (head == null) {
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while (cur != null) {
        mostRight = cur.left;
        if (mostRight != null) {
            while (mostRight.right != null && mostRight.right != cur) {
                mostRight = mostRight.right;
            }
            if (mostRight.right == null) {
                mostRight.right = cur;
                cur = cur.left;
                continue;
            } else {
                mostRight.right = null;
            }
        }
        // a、cur 如果没有左子树，先打印 cur 的值，然后 cur 向右移动
        // b、或者 cur 左子树上最右节点的右指针是指向 cur 的，先打印 cur 的值，然后 cur 向右移动
        System.out.print(cur.value + " ");
        cur = cur.right;
    }
}

后序遍历版本

// 后序遍历
public void morrisPost(Node head) {
    if (head == null) {
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while (cur != null) {
        mostRight = cur.left;
        if (mostRight != null) {
            while (mostRight.right != null && mostRight.ri
                mostRight = mostRight.right;
            }
            if (mostRight.right == null) {
                mostRight.right = cur;
                cur = cur.left;
                continue;
            } else {
                mostRight.right = null;
                printEdge(cur.left);
            }
        }
        cur = cur.right;
    }
    printEdge(head);
    System.out.println();
}
// 打印左子树的右边界时调用
public static void printEdge(Node head) {
    Node tail = reverseEdge(head); // 这个 tail 其实是反转之后的头
    Node cur = tail;
    while (cur != null) {
        System.out.print(cur.value + " ");
        cur = cur.right;
    }
    reverseEdge(tail); // 恢复反转的右边界
}
// 反转右边界
public static Node reverseEdge(Node from) {
    Node pre = null;
    Node next;
    while (from != null) {
        next = from.right; // 先把 next 保存起来
        from.right = pre; // 反转
        pre = from; // 更新 pre
        from = next; // 更新 from
    }
    return pre;
}

后序版本稍微有点复杂，主要是多了一个逆转左子树的右边界的做法。

测试 main 方法

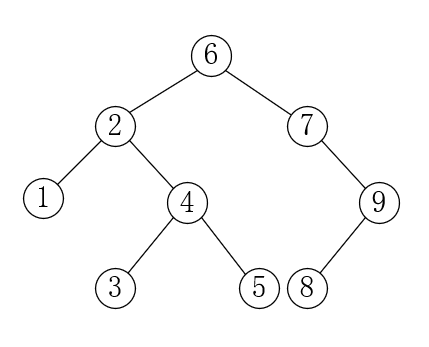
测试所用的二叉树

public static void main(String[] args) {
    // 构建测试用的二叉树
    Node head = new Node(6);
    head.left = new Node(2);
    head.left.left = new Node(1);
    head.left.right = new Node(4);
    head.left.right.left = new Node(3);
    head.left.right.right = new Node(5);
    head.right = new Node(7);
    head.right.right = new Node(9);
    head.right.right.left = new Node(8);
    // 测试
    Moris_5 ms = new Moris_5();
    ms.morrisPre(head);
    System.out.println("\n----------");
    ms.morrisIn(head);
    System.out.println("\n----------");
    ms.morrisPost(head);
}

输出

6 2 1 4 3 5 7 9 8 
----------
1 2 3 4 5 6 7 8 9 
----------
1 3 5 4 2 8 9 7 6