关于计数排序的稳定性及其对于基数排序的影响

前言

这篇博客的主要目的是记录以下对于计数排序稳定性及其对基数排序的影响的理解，故对于算法本身不会作详细描述。

计数排序的稳定性

在《算法导论》中，计数排序的大概思路是

• 1、利用一个辅助数组 C 记录原数组 A 的各个元素的计数
• 2、对辅助数组 C 进行处理，即 C[i] = C[i] + C[i - 1]
• 3、对原数组 A 从后往前依次进行重新放置元素到结果数组 B 中，使之到达有序状态

伪代码如下

下面我们具体来解释一下计数排序的稳定性问题。

首先，我们要弄清楚一件事情，就是稳定性的定义是什么？所谓排序的稳定性，是指如果数组中有重复的元素（值相等），那么数组在排完序的前后，这些重复的元素的相对位置保持不变。简单一点讲，就是，比如原来的数组 A 中有两个相等的元素 A[i] 和 A[j]，并且 A[i] 在 A[j] 的前面，那么，排完序之后，A[i] 还是在 A[j] 的前面。我们称能保持这种性质的排序是稳定的。

在上面的伪代码中，第 10 到 12 行，也就是最后处理数组的一步，对于 j，我们是从后往前进行遍历的，那么，这样可以保证排序是稳定的。

我们借助书中的例子来理解这一点。

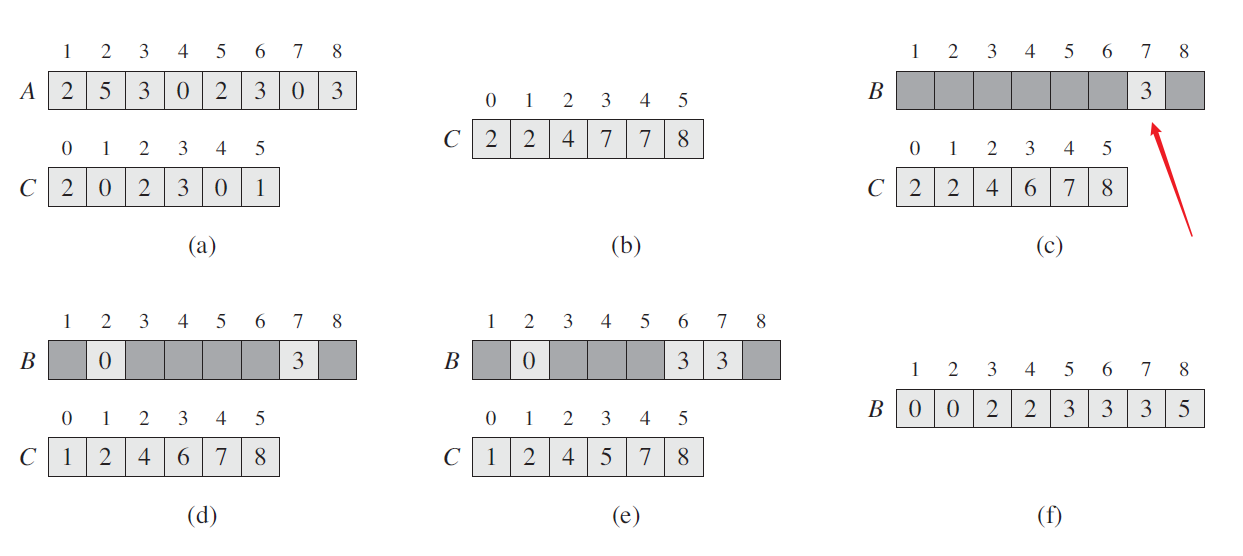
原数组 A 中有 3 个 3，我们假设排好序的数组中放置所有 3 的区域是 B[i..j]，那么，我们按照书中的次序，即从后往前往结果数组 B 中放置元素时，可以保证所有的 3 维持原来在 A 数组中的相对次序。

相应地，如果我们最后一步是从前往后处理数组的元素的话，那么，所有的 3 的相对位置会正好反过来。这与稳定性的要求相悖。

需要说明的一点是，对于计数排序本身，不管采用具有稳定性的排序或是采用不具有稳定性的排序，对于最后排序结果的正确性是没有影响的。

计数排序稳定性对于基数排序的影响

书上的基数排序是先按最低有效位进行排序的，排序的示例过程如下

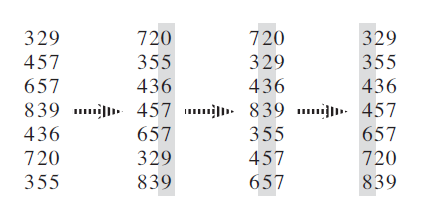
如果我们按照具有稳定性的计数排序，那么，很容易推出，基数排序是可以正常运转的。

然而，当我们采用另一种不具有稳定性的计数排序来给数据的每一位进行排序的话，那么最后排序的正确性是无法得到保证的。举个例子说明这一点：

我们假设有 4 个待排元素，当计数排序不稳定时，排序过程如下

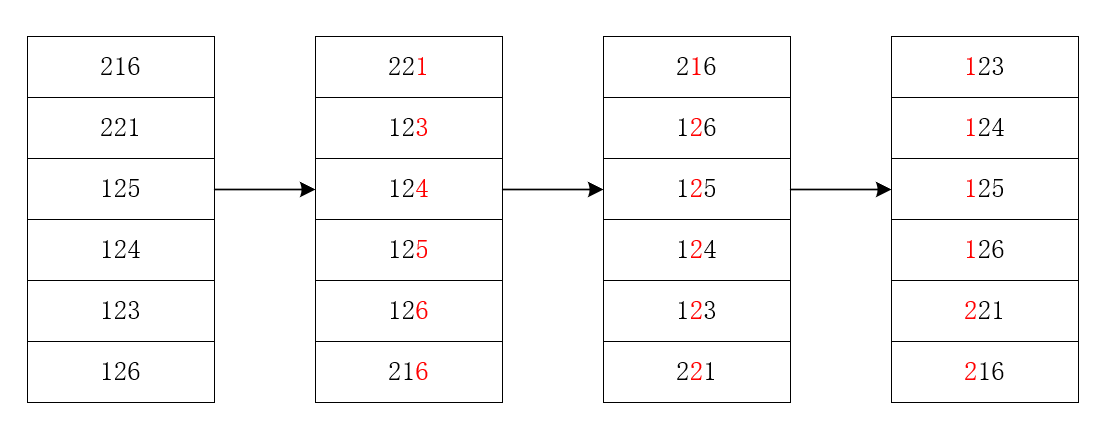
我们发现最后的结果是不对的。

我们只需要稍微回想一下基数排序的排序过程，应该就能明白针对单位数字排序的稳定性对于基数排序的重要性了。

计数排序的代码实现

计数排序的 Python 实现

def count_sort(A: list, B: list, k: int) -> None:
    '''
    计数排序
    :param A: 待排数组
    :param B: 排好序的结果数组
    :param k: A 中元素最大值
    :return: B
    '''
    C = []
    # 初始化 C 为 k + 1 个 0，索引是从 0 到 k
    for i in range(k + 1):
        C.append(0)
    for j in range(0, len(B)):
        C[A[j]] = C[A[j]] + 1 # 给数组 A 中的所有不同的数字计数
    for i in range(1, k + 1):
        C[i] = C[i] + C[i - 1] # 计算累加和
    # 按从后往前的顺序从 A 中取数据，然后根据规则放入 B 中
    for j in range(len(A) - 1, -1, -1):
        B[C[A[j]] - 1] = A[j] # 注意 B 的索引是从 0 开始的
        C[A[j]] = C[A[j]] - 1
    return None

# 测试
if __name__ == '__main__':
    A = [2, 5, 3, 10, 2, 3, 4, 3]
    B = [0 for i in range(len(A))]
    k = max(A)
    count_sort(A, B, k)
    print(B)
# output: [2, 2, 3, 3, 3, 4, 5, 10]