Python 实现经典排序算法（《算法导论》）

一、插入排序

1.1 算法描述

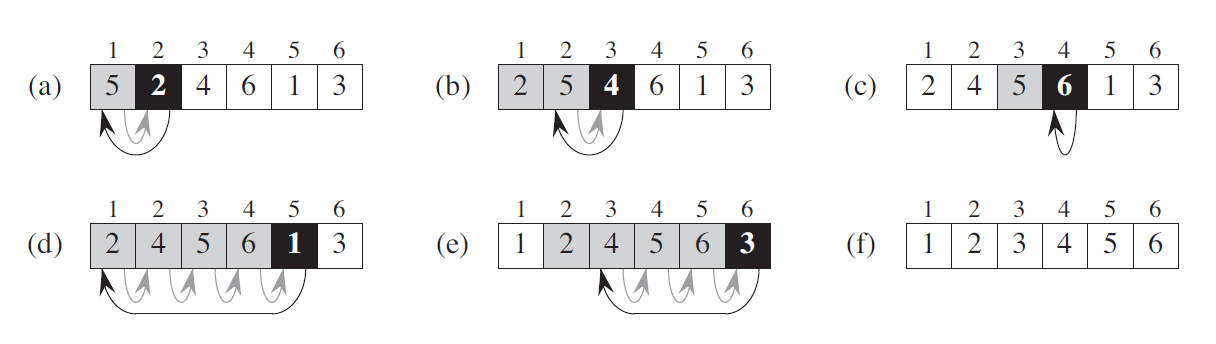
1.2 算法实现

# -*- coding: utf-8 -*-
# @File  : insertion_sort.py
# @Author: FanLu
# @Date  : 2021/4/25

'''
插入排序
'''

def insert_sort(A:list):
    '''
    插入排序
    :param A: 待排数组
    :return: None
    '''
    for j in range(1, len(A)):
        key = A[j]
        # 开始插入
        i = j  -1
        while i >= 0 and A[i] > key:
            A[i + 1] = A[i]
            i -= 1
        A[i + 1] = key

if __name__ == '__main__':
    A = [5, 2, 4, 6, 1, 3]
    insert_sort(A)
    print(A)

二、合并（归并）排序

2.1 算法描述

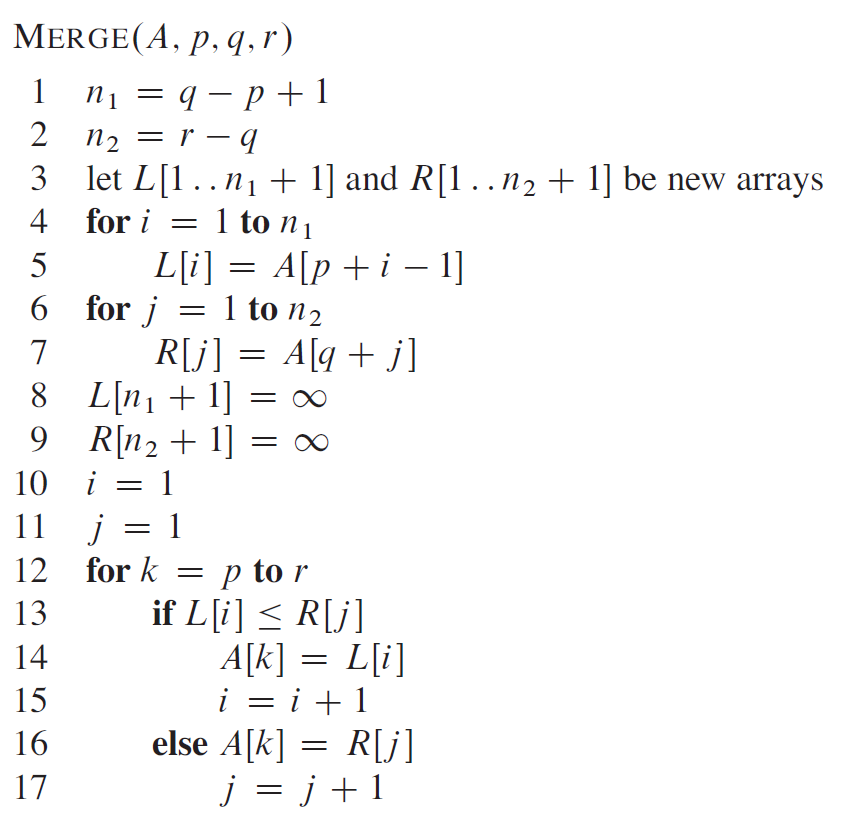
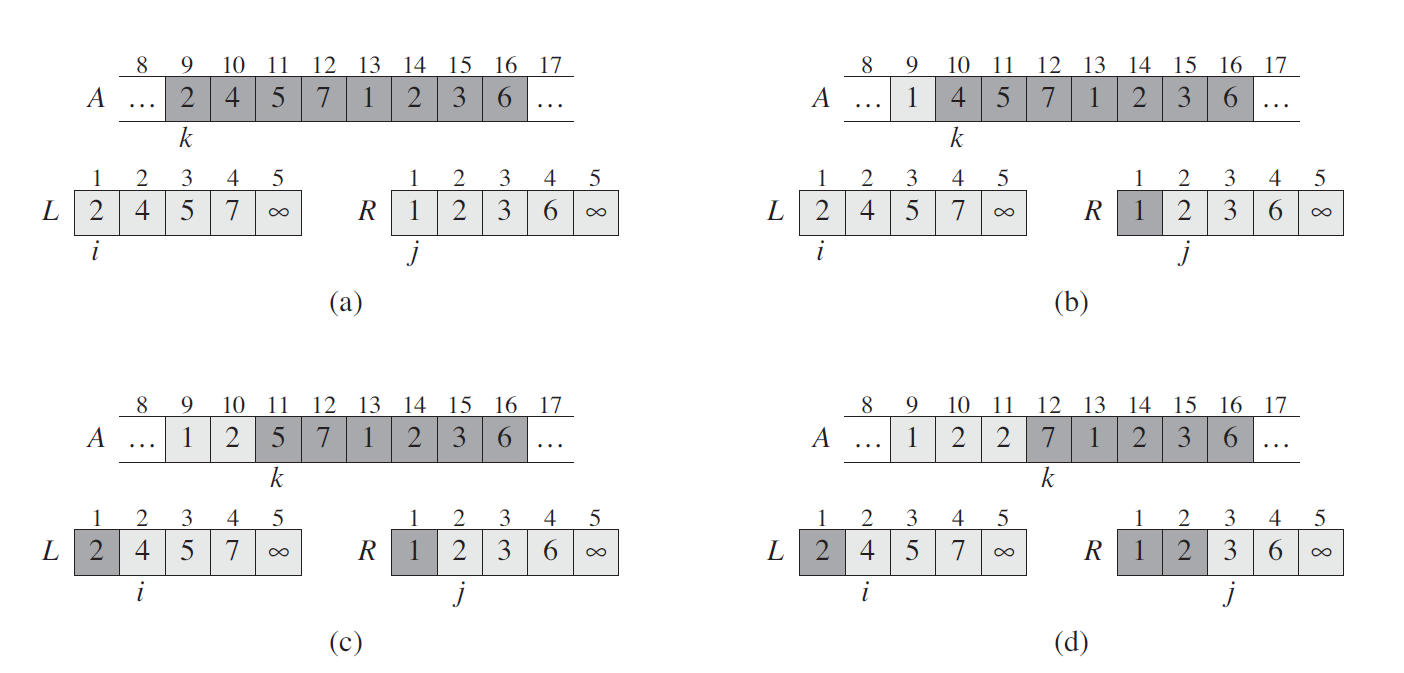
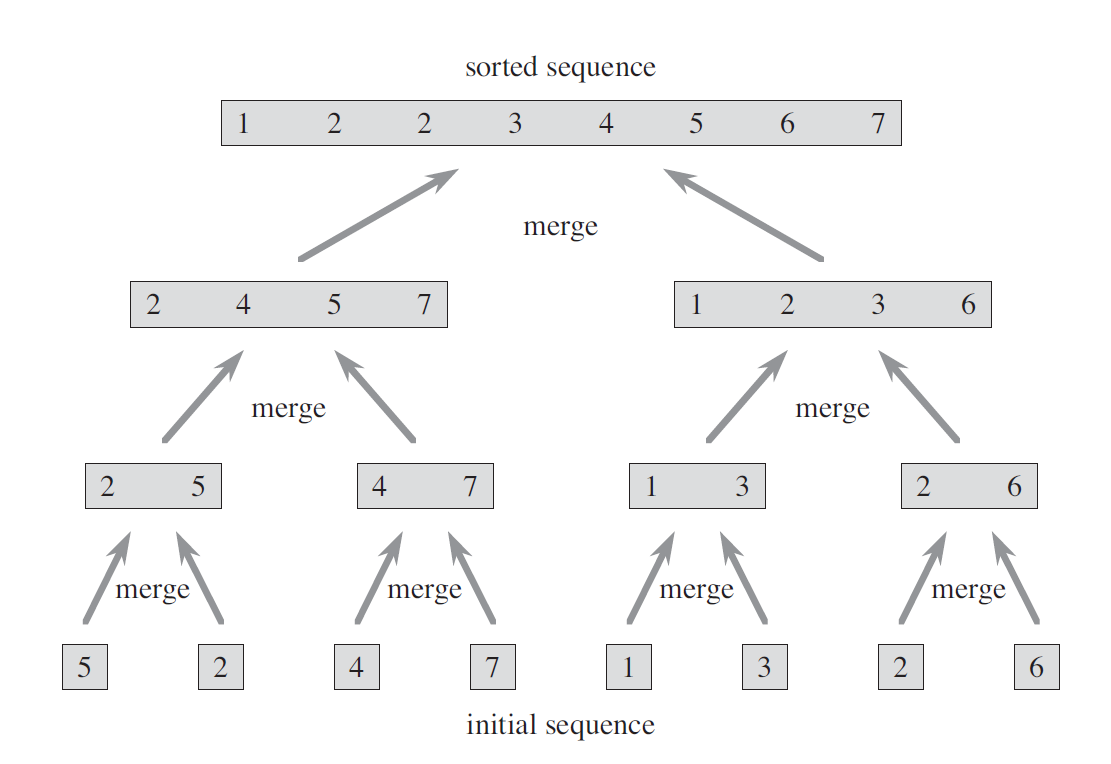
2.2 算法实现

# -*- coding: utf-8 -*-
# @File  : merge_sort.py
# @Author: FanLu
# @Date  : 2021/4/25

'''
合并（归并）排序
'''

# 归并函数
def merge(A:list, p:int, q:int, r:int):
    '''
    把数组的 p 到 q 和 q + 1 到 r 这两个部分进行合并
    :param A: 待排数组
    :param p: 左边的数组索引
    :param q: 中间的数组索引
    :param r: 右边的数组索引
    :return: None
    '''
    n_1 = q - p + 1 # 左边待归并的数组元素数量
    n_2 = r - q # 右边的待归并的数组元素数量
    # 这里多出来的一个元素放在最后，用正无穷来表示
    L = [0 for i in range(n_1 + 1)]
    R = [0 for i in range(n_2 + 1)]
    for i in range(n_1):
        L[i] = A[p + i]
    for j in range(n_2):
        R[j] = A[q + j + 1]
    L[n_1] = float('inf') # 给最后一个值赋无穷大
    R[n_2] = float('inf')
    i = 0
    j = 0
    for k in range(p, r + 1): # 这里注意索引的问题
        if L[i] <= R[j]:
            A[k] = L[i]
            i += 1
        else:
            A[k] = R[j]
            j += 1


def merge_sort(A:list, p:int, r:int):
    '''
    归并排序
    :param A: 待排数组
    :param p: 待排数组左边界
    :param r: 右边界
    :return: None
    '''
    if p < r:
        q = int((p + r) / 2)
        merge_sort(A, p, q)
        merge_sort(A, q + 1, r) # bug 处在了这里，这里第一次把 q 写成了 p ！！！！！
        merge(A, p, q, r)

if __name__ == '__main__':
    A = [5, 2, 4, 7, 1, 2, 3, 6]
    p = 0
    r = len(A) - 1
    merge_sort(A, p, r)
    print(A)

三、快速排序

3.1 算法描述

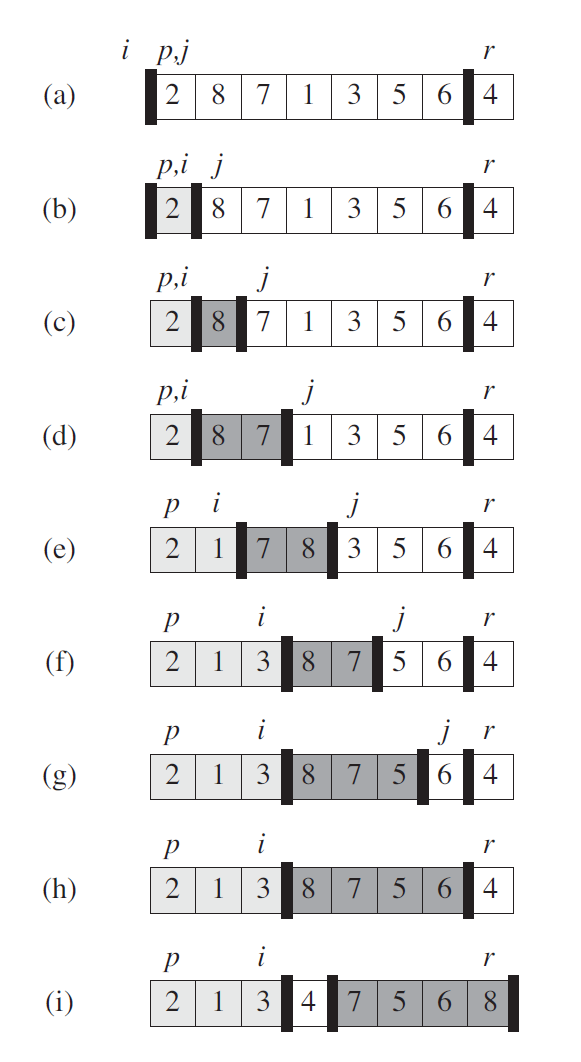
3.2 算法实现

# -*- coding: utf-8 -*-
# @File  : quick_sort.py
# @Author: FanLu
# @Date  : 2021/4/25

'''
快速排序
'''

def swap(A:list, i:int, j:int):
    tmp = A[i]
    A[i] = A[j]
    A[j] = tmp

def partition(A:list, p:int, r:int):
    '''
    处理 p 到 r 这一部分的数组（包含 r），具体操作是以 A[r] 为中心点（pivot），
    将小于等于 pivot 的元素放在左边，将大于 pivot 的元素放在右边
    :param A: 待排数组
    :param p: 左边界索引
    :param r: 右边界索引
    :return: None
    '''
    x = A[r] # pivot 值
    i = p - 1
    for j in range(p, r): # j 从 p 到 r（不包含 r）
        if A[j] <= x:
            i = i + 1 # i + 1 之后指向的就是右边的比 pivot 值大的那部分数组中的第一个元素
            swap(A, i, j)
    swap(A, i + 1, r) # 把 pivot 值给换回来
    return i + 1 # i + 1 是中间值

def quick_sort(A:list, p:int, r:int):
    '''
    快速排序
    :param A: 待排数组
    :param p: 左边界索引
    :param r: 右边界索引
    :return: None
    '''
    if p < r:
        q = partition(A, p, r)
        quick_sort(A, p, q - 1)
        quick_sort(A, q + 1, r)

if __name__ == '__main__':
    A = [2, 8, 7, 1, 3, 5, 6, 4]
    p = 0
    r = len(A) - 1
    quick_sort(A, p, r)
    print(A)

四、随机快速排序算法

4.1 算法描述

4.2 算法实现

# -*- coding: utf-8 -*-
# @File  : random_quick_sort.py
# @Author: FanLu
# @Date  : 2021/4/25

'''
随机快速排序
'''

import quick_sort
import random

def randomized_partition(A:list, p:int, r:int):
    '''
    随机化选择 pivot
    :param A: 待排数组
    :param p: 左边界索引
    :param r: 右边界索引
    :return: None
    '''
    i = random.randint(p, r)
    quick_sort.swap(A, r, i)
    return quick_sort.partition(A, p, r)

def randomized_quicksort(A:list, p:int, r:int):
    '''
    随机化快速排序
    :param A: 待排数组
    :param p: 左边界索引
    :param r: 右边界索引
    :return: None
    '''
    if p < r:
        q = randomized_partition(A, p, r)
        randomized_quicksort(A, p, q - 1)
        randomized_quicksort(A, q + 1, r)

if __name__ == '__main__':
    A = [2, 8, 7, 1, 3, 5, 6, 4]
    p = 0
    r = len(A) - 1
    randomized_quicksort(A, p, r)
    print(A)

五、计数排序

5.1 算法描述

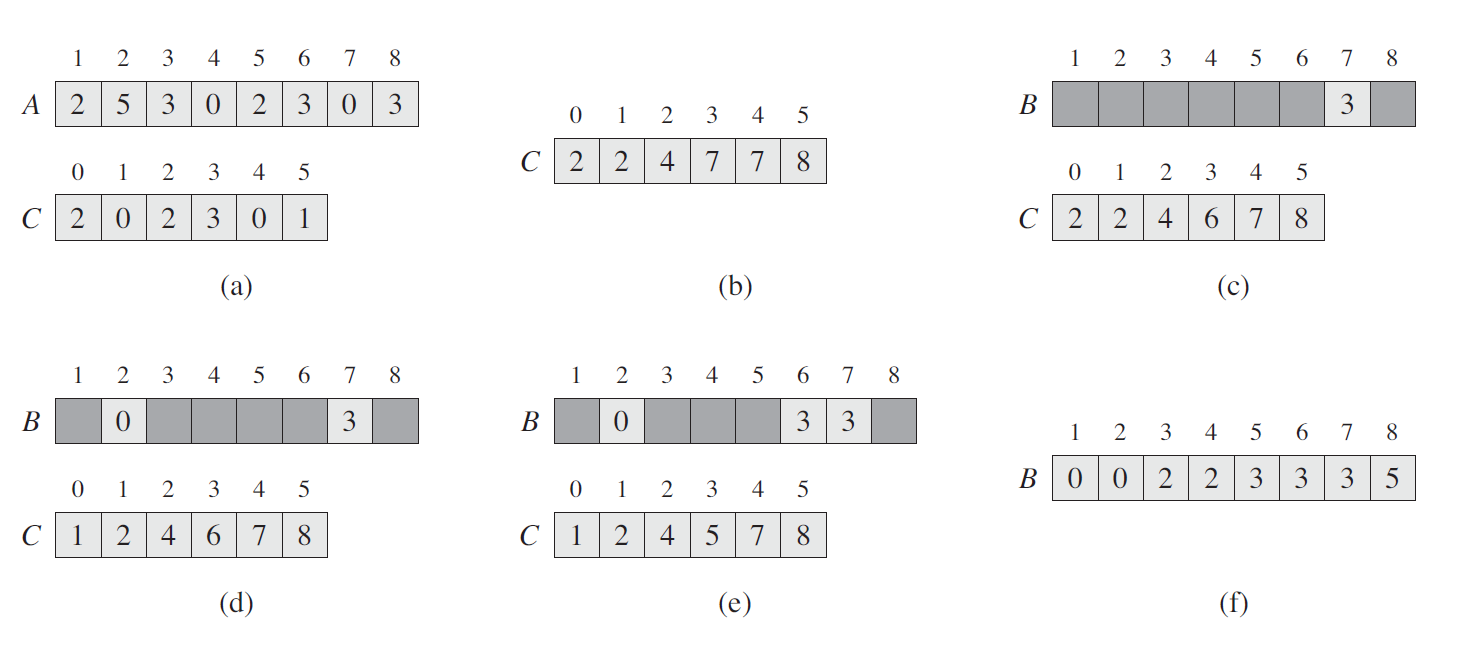
上图是 COUNTING-SORT 在输入数组 A[1..8] 上的处理过程，其中 A 中的每一个元素都是不大于 k = 5 的非负整数。(a) 是第 5 行执行后的数组 A 和辅助数组 C 的情况。(b) 是第 8 行执行后，数组 C 的情况。(c)~~(e) 分别显示了第 10~~12 行的循环体迭代了一次、两次和三次之后，输出数组 B 和辅助数组 C 的情况。其中，数组 B 中只有浅色阴影部分有元素值填充。(f) 是最终排好序的数组 B。

这里，(a) 中的 C 数组是计数数组，即记录待排数组中每个数字出现的次数，它的 size 是 A 中最大元素加一，因为它的索引对应的就是 A 中元素的值。(b) 中的 C 数组是 (a) 中的 C 数组中元素从左到右依次累加的结果。

最后往 B 数组中放置元素时，是从 A 中按照倒序的方式依次取元素，再放入 B 中相应的位置的。

5.2 算法实现

# -*- coding: utf-8 -*-
# @File  : counting_sort.py
# @Author: FanLu
# @Date  : 2021/4/25

'''
计数排序
'''

def counting_sort(A: list, B: list, k: int):
    '''
    计数排序
    :param A: 待排数组
    :param B: 排好序的结果数组
    :param k: A 中元素最大值
    :return: None
    '''
    C = []
    # 初始化 C 为 k + 1 个 0，索引是从 0 到 k
    for i in range(k + 1):
        C.append(0)
    for j in range(0, len(B)):
        C[A[j]] = C[A[j]] + 1 # 给数组 A 中的所有不同的数字计数
    for i in range(1, k + 1):
        C[i] = C[i] + C[i - 1] # 计算累加和
    # 按从后往前的顺序从 A 中取数据，然后根据规则放入 B 中
    for j in range(len(A) - 1, -1, -1):
        B[C[A[j]] - 1] = A[j] # 注意 B 的索引是从 0 开始的
        C[A[j]] = C[A[j]] - 1

if __name__ == '__main__':
    A = [2, 5, 3, 10, 2, 3, 4, 3]
    B = [0 for i in range(len(A))]
    k = max(A)
    counting_sort(A, B, k)
    print(B)

六、桶排序

6.1 算法描述

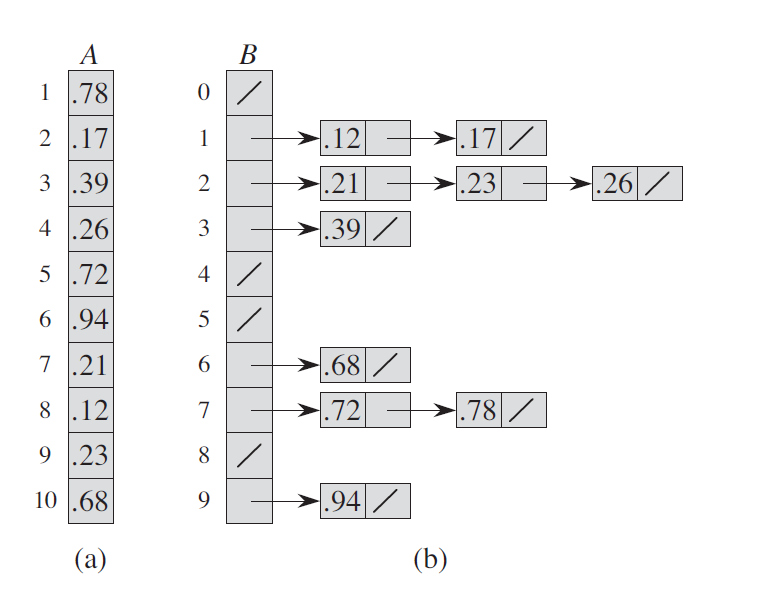
6.2 算法实现

# -*- coding: utf-8 -*-
# @File  : bucket_sort.py
# @Author: FanLu
# @Date  : 2021/4/25

'''
桶排序，这里假设待排元素的范围是 [0, 1)（前闭后开）
'''

import insertion_sort

def bucket_sort(A:list):
    '''
    桶排序
    :param A: 待排数组
    :return: None
    '''
    n = len(A)
    B = []
    for i in range(n):
        B.append([])
    for i in range(n):
        index = int(n * A[i])
        B[index].append(A[i])
    for i in range(n):
        insertion_sort.insert_sort(B[i])
    k = 0
    for i in range(n):
        for each in B[i]:
            A[k] = each
            k = k + 1

if __name__ == '__main__':
    A = [0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.12, 0.23, 0.68]
    bucket_sort(A)
    print(A)

七、算法效率可视化

主要是利用 Python 的 matplotlib 这个库，绘制 $T(N)$ 随输入规模的变化的折线图，这里同时绘制三种情况：最好情况（正序）、一般情况和最坏情况（逆序）。

# -*- coding: utf-8 -*-
# @File  : time_analysis.py
# @Author: FanLu
# @Date  : 2021/4/25

import insertion_sort, merge_sort
import quick_sort, random_quick_sort
import counting_sort, bucket_sort
import time
import random
import matplotlib.pyplot as plt

A = [10, 20, 30, 50, 100, 500, 1000, 2000, 3000, 4000, 5000, 6000, 7000]
# A = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100] # 测试数据
T = []
T_best = []
T_worst = []
T_list = [T, T_best, T_worst]
for i in A:
    B = []
    for j in range(i):
        B.append(random.randint(0, i))
    B_best = sorted(B)
    B_worst = B_best[::-1]
    B_list = [B, B_best, B_worst]
    TB_map = [(T, B), (T_best, B_best), (T_worst, B_worst)]
    for each_T, each_B in TB_map:
        pre = time.process_time_ns()
        insertion_sort.insert_sort(each_B)
        after = time.process_time_ns()
        print(after - pre)
        each_T.append(after - pre)
print(T)
print(T_best)
print(T_worst)
# 绘制图线
plt.plot(A, T, label='normal')
plt.plot(A, T_best, label='best')
plt.plot(A, T_worst, label='worst')
plt.legend() # 显示 label
plt.savefig(fname='insert.svg', format='svg')
plt.show()

这里只绘制了一个插入排序，如果想绘制其他的图像，只需要将代码中的相应的排序方法给替换掉，然后重新跑一遍代码即可。不过，在实际测试时，如果要替换成其他的排序算法来测试，那么，相应地也要调整测试数据（也就是输入的规模），否则快速排序在最坏情况下的递归会耗尽内存。

更新（2021.07.09）：在 StackOverflow 找到了一个说法，Python 的递归限制是 999 个调用栈，而且，Python 中似乎没有真正的递归。所以，这个快速排序在 Python 中似乎能用递归实现。然后，我测试了一下 Java 的极限，原来也不是很行啊，到了 100,000 这个级别，就会 StackOverflow 了。

总结

关于这些排序算法，基本都是直接对原数组进行操作的，原因是这里要测试它们的时间效率，所以不便于产生其他额外的开销。但是，在实际运用中，也会有对待排数组的副本进行排序然后返回的情况，这样的好处是不会修改待排的原数组，这一点是要注意的。

算法设计与分析

#算法 #《算法导论》 #算法设计与分析实验一

Python 实现经典排序算法（《算法导论》）

http://fanlumaster.github.io/2021/04/26/Python-实现经典排序算法（《算法导论》）/

作者

fanlumaster

发布于

2021年4月26日

许可协议

常用门电路符号及表达式上一篇

解决 Windows 命令行：'cl' 不是内部或外部命令下一篇