计算机补码一位乘法

补码乘法由英国人布斯（Booth）于 1950 年发明，又称为布斯（Booth）算法。

1、Booth 算法的推导

设 $[x]{补} = x_0.x_1x_2…x_n$，$[y]{补} = y_0.y_1y_2…y_n$。下面分两种情况来推导 Booth 算法。

(1) 设被乘数 $x$ 符号任意，乘数 $y$ 符号为正，则：

$$
[x]{补} = x_0.x_1x_2…x_n \quad [y]{补} = 0.y_1y_2…y_n
$$

根据补码的定义：

$$
\begin{equation}
\begin{split}
&[x]{补} = (2 + x) ; mod ; 2 = (2^{n + 1} + x) ; mod ; 2（注 1） \
&[y]{补} = y
\end{split}
\end{equation}
$$

$$
\begin{equation}
\begin{split}
[x]{补} \times [y]{补} &= [(2^{n + 1} + x) ; mod ; 2] \times y \
&= [(2^{n + 1} + x) \times y] ; mod ; 2 \
&= (2^{n + 1} \times y + x \times y) ; mod ; 2 \
&= (2 \times y_1y_2…y_n + x \times y) ; mod ; 2 \
&（这一块的证明见注 2）
\end{split}
\end{equation}
$$

所以，

$$
\begin{matrix}
[x]{补} \times [y]{补} = (2 + x \times y) ; mod ; 2 = [x \times y]{补} \
[x \times y]{补} = [x]_{补} \times y \qquad \qquad (1)
\end{matrix}
$$

(2) 被乘数 $x$ 符号任意，乘数 $y$ 符号为负，则根据补码定义：

$$
[x]{补} = x_0.x_1x_2…x_n \quad [y]{补} = 1.y_1y_2…y_n = 2 + y
$$

所以：

$$
\begin{matrix}
y = [y]_{补} - 2 = 1.y_1y_2…y_n - 2 = 0.y_1y_2…y_n - 1 \
x \times y = x \times (0.y_1y_2…y_n - 1) = x \times 0.y_1y_2…y_n - x \qquad \qquad (2)
\end{matrix}
$$

对式 (2) 两边同时求补，并利用补码减法公式展开等式右边项可得：

$$
[x \times y]{补} = [x \times 0.y_1y_2…y_n]{补} - [x]_{补} \qquad \qquad (3)
$$

根据式 (1) 可得：

$$
[x \times y]{补} = [x]{补} \times 0.y_1y_2…y_n - [x]_{补} \qquad \qquad (4)
$$

将式 (1) 和式 (4) 综合起来，引入 $y_0$ 位，即可得补码一位乘法的统一算式，即：

$$
[x \times y]{补} = [x]{补} \times 0.y_1y_2…y_n - [x]_{补} \times y_0 \qquad \qquad (5)
$$

对于式 (5) 右边第二项 $[x]_{补} \times y_0$，存在如下结论：

当 $y$ 为正时，$y_0 = 0$，该项不存在；当 $y$ 为负时 $y_0 = 1$，该项为 $[x]_{补}$。

总结下来，就是以下的式子：

$$
\begin{equation}
\begin{split}
&[x \times y]{补} = [x]{补} \times y & \quad y ; 符号为正 \
&[x \times y]{补} = [x]{补} \times 0.y_1y_2…y_n - [x]_{补} & \quad y 符号为负
\end{split}
\end{equation}
$$

$$
[x \times y]{补} = [x]{补} \times 0.y_1y_2…y_n - [x]_{补} \times y_0 \quad 不考虑 ; y ; 的符号
$$

接下来是推导从式 (5) 演变成适合计算机计算的迭代公式。

为了方便，我们把上面的式 (5) 放在这里：

$$
[x \times y]{补} = [x]{补} \times 0.y_1y_2…y_n - [x]_{补} \times y_0
$$

上面的式子可以展开成下面的形式：

$$
[x \times y]{补} = [x]{补} \times [(y_1 - y_0) + 2^{-1}(y_2 - y_1) + 2^{-2}(y_3 - y_2) + \cdots + 2^{-(n - 1)}(y_n - y_{n - 1}) + 2^{-n}(0 - y_n)]
$$

然后，设 $[z_0]_{补} = 0$，接着，

$$
\begin{equation}
\begin{split}
[z_1]{补} &= 2^{-1} { [z_0]{补} + (y_{n + 1} - y_n)[x]{补} } \
[z_2]{补} &= 2^{-1} { [z_1]{补} + (y{n} - y_{n - 1})[x]{补} } \
\cdots &\cdots \
[z_n]{补} &= 2^{-1} { [z_{n - 1}]{补} + (y{2} - y_1)[x]{补} } \
[x \times y]{补} &= [z_{n + 1}]{补} = 2^{-1} { [z_n]{补} + (y_1 - y_0)[x]_{补} } \
\end{split}
\end{equation}
$$

上面的推导可以类比于高中时候学过的二项式：

$$
\begin{aligned}
f(x) &= a_0 + a_1x + a_2x^2 + a_3x^3 \
&= a_0 + x(a_1 + x(a_2 + x(a_3 + 0)))
\end{aligned}
$$

$$
\begin{aligned}
S_0 &= 0 \
S_1 &= x(S_0 + a_3) \
S_2 &= x(S_1 + a_2) \
S_3 &= x(S_2 + a_1) \
S_4 &= S_3 + a_0
\end{aligned}
$$

当然，其中有一点差异，就是我们的式子中，比如说

$$
[z_1]{补} = 2^{-1} { [z_0]{补} + (y_{n + 1} - y_n)[x]_{补} }
$$

有一项 $(y_{n + 1} - y_n)$ 的后面还乘上了一个 $[x]{补}$，这个我一开始也不理解，后来经同学点拨，我决定将推导过程中的前几个式子给展开看一下，结果发现每一个式子都可以把 $[x]{补}$ 给提出来，那么，这个问题自然就解决了。

算法描述

• 在 $[y]{补}$ 后添一个 $0$ 作为 $y{n + 1}$，令部分积为 $0$
• 如果 $y_{n + 1} = y_n$，部分积 $+ ; 0$，并将结果右移一位
• 如果 $y_{n + 1} < y_n$，部分积 $+ ; [-x]_{补}$，并将结果右移一位
• 如果 $y_{n + 1} > y_n$，部分积 $+ ; [x]_{补}$，并将结果右移一位

2、举例应用

已知 $X = +0..1101$，$Y = +0.1011$，用补码一位乘法求 $X \times Y$.

$$
解：[X]{补} = 0.1101 \quad [Y]{补} = 0.1011 \quad [-X]_{补} = 1.0011
$$

$$
\begin{equation}
\begin{split}
&部分积 \qquad & 乘数 \qquad \quad & 说明 \
&00.0000 \qquad & 0.10110 & \
{+} ; &11.0011 \qquad & & Y_{n + 1} < Y_n, 部分积 +[-X]{补} \
···& ········& & \
&11.0011 \qquad & & \
\rightarrow ; &11.1001 \qquad & 1001011 & 将结果右移一位 \
{+} ; &00.0000 \qquad & & Y_{n + 1} = Y_n, 部分积 + 0 \
···& ········ & & \
&11.1001 \qquad & & \
\rightarrow ; &11.1100 \qquad & 11.0101 & 将结果右移一位 \
{+} ; &00.1101 \qquad & & Y_{n + 1} > Y_n, 部分积 + [X]{补} \
···& ········ & & \
&00.1001 \qquad & & \
\rightarrow ; &00.0100 \qquad & 111.010 & 将结果右移一位 \
{+} ; &11.0011 \qquad & & Y_{n + 1} < Y_n, 部分积 + [-X]{补} \
···& ········ & & \
&11.0111 \qquad & & \
\rightarrow ; &11.1011 \qquad & 1111.01 & 将结果右移一位 \
{+} ; &00.1101 \qquad & & Y_{n + 1} > Y_n, 部分积 + [X]{补} \
···& ········ & & \
&00.1000 \qquad & &
\end{split}
\end{equation}
$$

所以

$$
\begin{equation}
\begin{split}
[XY]_{补} &= 0.10001111 \
XY &= 0.10001111
\end{split}
\end{equation}
$$

---

注释：

1、小数的补码，按照定义应该是：

设二进制小数 $X = \pm 0.x_{-1}x_{-2}…x_{-m}$，则其补码定义为

$$
[X]_{补} =
\left{\begin{matrix}
\begin{aligned}
&X & 0 & \leqslant X < 1 \
&2 + X & -1 & \leqslant X < 0 \
\end{aligned}
\end{matrix}\right.
$$

上面的式子可以归结成一个式子：

$$
[X]_{补} = (2 + X) ; mod ; 2 \qquad -1 \leqslant X < 1
$$

2、在上面的推导过程中，隐含地用了下面的关系：

设 $ -1 < x, y < 1 $，则有

$$
[(2^{n + 1} + x) ; mod ; 2] \times y = [(2^{n + 1} + x) \times y] ; mod ; 2
$$

下面我门来证明这个式子。

(1) $x \in (0, 1)$，

$$
左式 = x \times y
$$

对于模运算，有这样的运算法则：

$$
(a \times b) ; mod ; p = [(a ; mod ; p) \times (b ; mod ; p)] ; mod ; p
$$

所以有

$$
[(2^{n + 1} + x) ; mod ; 2 \times y ; mod ; 2] ; mod ; 2 = (x \times y) ; mod ; 2 = x \times y
$$

所以有 $左式 = 右式$。

(2) $x \in (-1, 0)$，

$$
左式 = (2 + x) \times y
$$

$$
右式 = [(2 + x) \times y] ; mod ; 2 = (2 + x) \times y
$$

所以有 $左式 = 右式$。

综上，原式的正确性得证。

对于边界情况，即 $x = 0 ; or ; 1 ; or ; -1$ 时候，我想，计算机应该有更好的方法直接就把结果给计算出来了，这里就不再赘述。

3、电路图逻辑实现

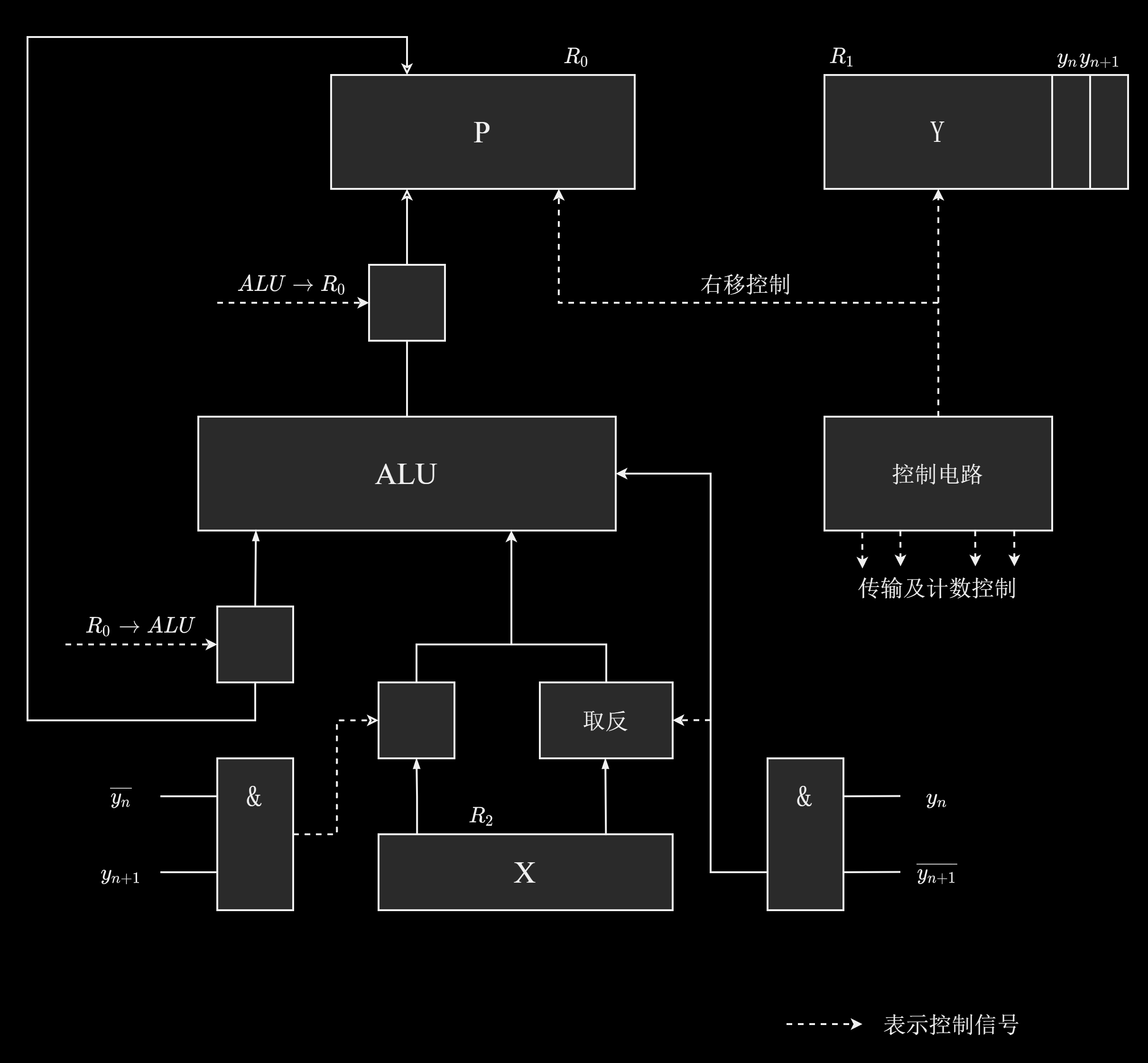
首先说明一下正方形方框充当的是缓冲器的角色。

然后，解释一下下面的部分：

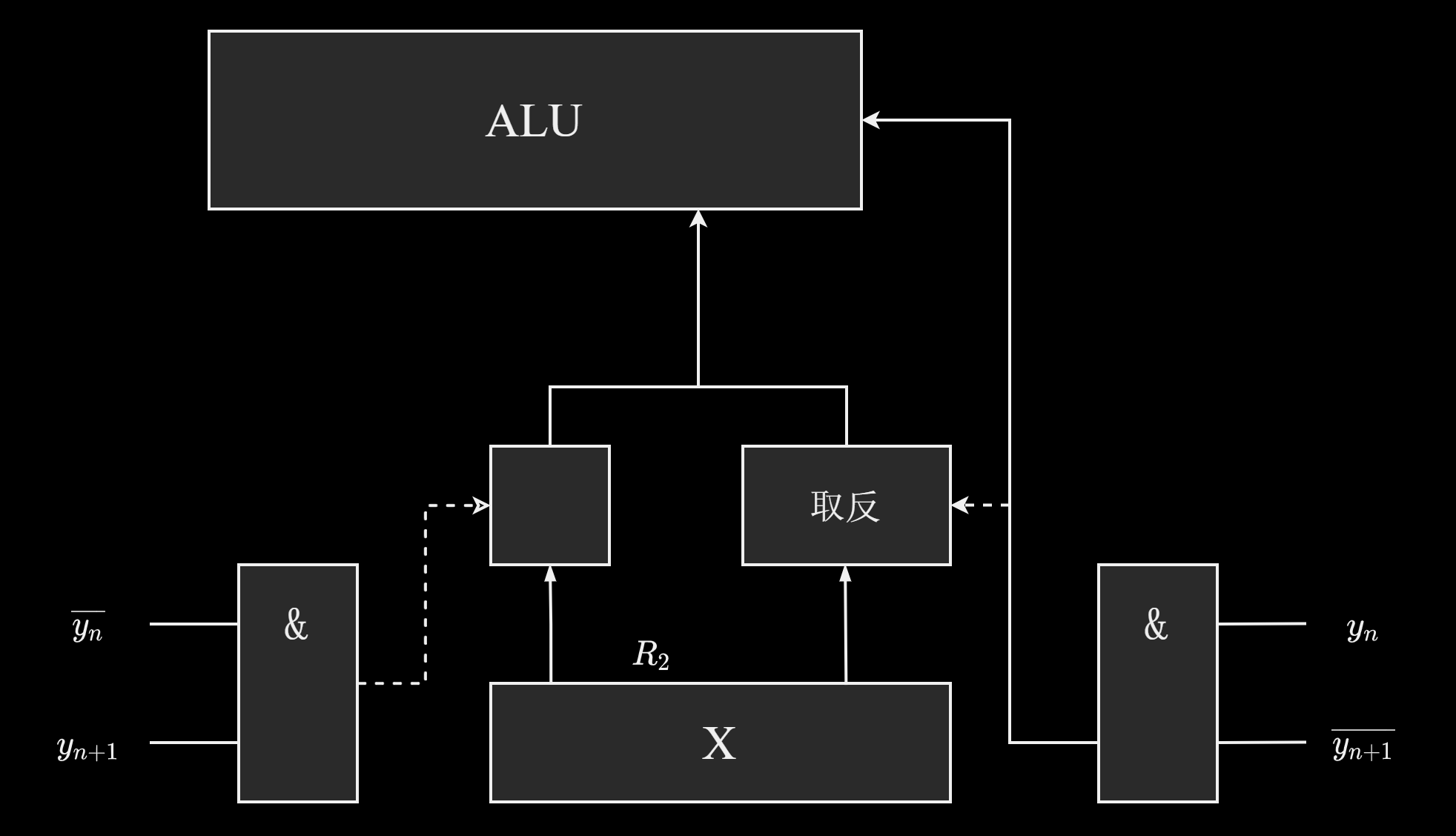
• 左边，当 $y_{n + 1} > y_n$ 时，与门输出为 1，这时，X 直接送上去；
• 右边，当 $y_{n + 1} < y_n$ 时。与门输出为 1，这时，X 按位取反加一，利用的是：$[-X]{补} = [X]{补}$ 先按位取反然后在末尾加一。

然后，图中的 $R_0, ; R_1$ 表示的寄存器（Register），在实际运作过程中，P 和 Y 都要移位。

最后，这个图仅仅是逻辑实现的示意图，其中还是隐藏了一些具体的细节的。